We should have basic knowledge on the representation of two dimensional matrix in C. Here is three two dimensional matrix a, b and c. a for matrix A, b for matrix B, and c for matrix C. which holds the multiplication result. i, j, k are control variable and sum is needed to hold the summation of the consecutive two products.
#include <stdio.h>
int main()
{
int a[2][2] = {3,4,2,7};
int b[2][2] = {6,8,5,9};
int c[2][2], i, j, k, sum;
printf("Matrix A is : \n\t\t");
for(i=0;i<2;i++){
for(j=0;j<2;j++){
printf("%d \t",a[i][j]); }
printf("\n\t\t");
}
printf("\nMatrix B is : \n\t\t");
for(i=0;i<2;i++){
for(j=0;j<2;j++){
printf("%d \t",b[i][j]);
}
printf("\n\t\t");
}
printf("\nMultiplication of matrix A and B\n\t\t");
for(i=0;i<2;i++){
for(j=0;j<2;j++){
sum = 0;
for(k=0;k<2;k++){
sum = sum + a[i][k] * b[k][j];
}
c[i][j]=sum;
}
}
printf("\nMatrix A*B is : \n\t\t");
for(i=0;i<2;i++){
for(j=0;j<2;j++){
printf("%d \t",c[i][j]);
}
printf("\n\t\t");
}
return 0;
}
Traversing a matrix
Let us consider the traversing of matrix A, we use here two for loop. One is nested in another, now consider for the first time printf("%d \t",a[i][j]); at the first time i and j enter the loop with value i=0 and j=0; so it represent the first element of matrix A with a[0][0]=3, After the first iteration j increase it's value by j =1 and the inner loop is also true in this case so it point a[0][1] = 4; At the next iteration j= 2 so the for loop is false as 2 is not greater than 2. so it execute the next line printf("\n\t\t"); which prints a new line and two tab after printing a[0][0]=3 and a[0][1] =4,
Now lets talk about the outer loop, for(i=0;i<2;i++) by this time i = 1 and then it enter the inner loop for(j=0;j<2;j++) again it runs two times and results a[1][0]=2 and a[1][1]=7.
Graphical Representation of matrix multiplication
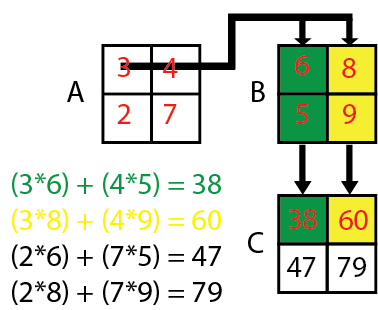
Matrix Multiplication
It uses three for loops, the control variables are i, j, k, at the first iteration all these control variables including sum are zero so,
sum = sum + a[i][k] * b[k][j]
=> 0+a[i][k] * b[k][j]
=> 0+ a[0][0]=3 * b[0][0]= 6
=> 3*6=18
so sum =18, At the next iteration k=1, and still i=0 also j=0 therefore
sum = sum + a[i][k] * b[k][j]
=> 18+a[0][1]*b[1][0]
=>18+4*5
=>18+20
=38
At the next iteration k gets 2 so it becomes false and go to the upper loop (control variable j) and brings j=1, and still i=0, and sum initialize with 0;
sum = sum + a[i][k] * b[k][j]
=> 0 + a[i][k] * b[k][j]
=> 0 + a[0][0]=3 * b[0][1]= 8
=> 3*8=24,
At the next iteration k=1, therefore
sum = sum + a[i][k] * b[k][j]
=> 24+a[0][1]*b[1][1]
=> 24+4*9
=> 24+36=60.
And thus 47, 97 comes correspondingly.
Exception
From the above program we can see that the column of matrix A and the row of matrix B are equal 2=2,This rule must be maintain in matrix multiplication
Column number of first matrix must be equal to the row number of the second matrix
Now lets try with another programm
#include <stdio.h>
int main()
{
int a[12][12], b[12][12] ,c[12][12], rowa, cola, rowb,colb, i, j, k, sum;
printf("Row of the first matrix\n");
scanf("%d",&rowa);
printf("Column of the first matrix(a) \n");
scanf("%d",&cola);
printf("Enter the elements of first matrix\n");
for ( i = 0 ; i < rowa ; i++ ){
for ( j = 0 ; j < cola ; j++ ){
scanf("%d", &a[i][j]);
}
}
printf("Row of the second matrix\n");
scanf("%d",&rowb);
printf("Column of the second matrix(b) \n");
scanf("%d",&colb);
if(cola != rowb){
printf("The row number of the second matrix(b) should be %d\n",cola);
printf("Column of first matrix must be equal to the number of row of the second matrix.\n");
printf("Run the program again.\n");
}
else{
printf("Enter the elements of second matrix\n");
for ( i = 0 ; i < rowb ; i++ ){
for ( j = 0 ; j < colb ; j++ ){
scanf("%d", &b[i][j]);
}
}
printf("\nMultiplication of matrix A and B\n\t\t");
for(i=0;i<rowa;i++){ // rowa ...? [1]
for(j=0;j<colb;j++){ // colb...? [2]
sum = 0;
for(k=0;k<rowb;k++){// rowb...? [3]
sum = sum + a[i][k] * b[k][j];
}
c[i][j]=sum;
}
}
printf("\nMatrix A*B is : \n\t\t");
for(i=0;i<rowa;i++){
for(j=0;j<colb;j++){
printf("%d \t",c[i][j]);
}
printf("\n\t\t");
}
}
return 0;
}
- The number of row of the product matrix is equal to the row of the first(a) matrix
- The number of column of the product matrix is equal to the second(b) matrix
- The iteration number is equal to row of the second matrix (rowb) or the column of the first matrix (cola), since both are equal.