C program For Trigonometric ratio.

By : Milon

On : 9:10 PM

Lets try with the library function to calculate the trigonometric ratio. Here use the built in function. The C library function double cos(double x) returns the cosine of a radian angle x. Correspondingly the sin(x) and tan(x)

Here we just convert the degree in radian using 180⁰ = π^c (Radian)

// Using Library function
#include<stdio.h>
void main(){
    float tempt, degree;
    printf("Enter the number \(In degree\)\n");
    scanf("%f",&degree);
    tempt = degree;
    degree = degree * 3.14159265359 / 180;
    printf("sin\(%.2f\) = %1.2f\n",tempt, sin(degree));
    printf("cos\(%.2f\) = %1.2f\n",tempt, cos(degree));
    printf("tan\(%.2f\) = %1.2f\n",tempt, tan(degree));


}

Now try with Taylor and Maclaurin Series Following are these equations.. we will transform them in our program.

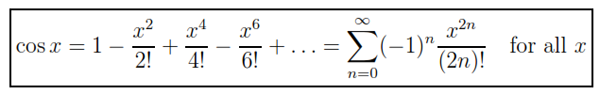
#include<math.h>
#include<stdio.h>
double  factorial(int num){
        double fact =1;
        int i;
        for(i=1;i<=num;i++){
            fact = fact*i;
        }

        return fact;
}

void main(){
    double tempt, x,sum=1.0;
    int term,counter;
    int  sign =-1.0;
    printf("Enter the term number till you want to calculate the value\n");
    scanf("%d",&term);
    printf("Enter the value of x\n");
    scanf("%lf",&x);
    tempt=x;

//ex
    for(counter=1;counter <= term ; counter++){
        sum = sum + ((pow(x,counter))/(factorial(counter)));
    }
 printf("So the Taylor series of ex around %.1lf is %.15lf \n",tempt,sum);

//sinx
x = x * 3.14159265359 / 180;
sum = x;
for(counter=3;counter<=term;counter+=2){
   sum = sum + (sign * (pow(x,counter))/factorial(counter));
}
printf("The Taylor series of sin(x) around %.1lf is %.15lf \n",tempt,sum);


// cosx
 sum = 1.0;
 sign = -1.0;
 for(counter=2;counter <= term ; counter += 2){
        sum = sum + (sign *(pow(x,counter))/factorial(counter));
        sign = sign * (-1);
    }
 printf("The Taylor series of cos(x) around %.1lf is %.15lf \n",tempt,sum);


}

Explanation

Here we use a user defined function factorial which takes an integer value to calculate it's factorial and the function also return a double type integer.

Here we use some variables
x = the variable of Taylor series.
sum = to hold the value of cos, sin and e^x
tempt = to hold the value of x, as we change the value of x into radian.
term = Number of term of Taylor series.
counter = loop counter.
sign = to make negative number.

---

e^x

We initialize the sum with 1, and the series of e^x also start with 1 then just use it's corresponding arithmetic expression

sin(x)

Again we initialize the sum with 1 since the series of cos(x) start with 1, the counter variable start with 2 and each time it increases by 2, as the series goes. and the sign variable also changes its negativity after each iteration.

cos(x)

Notice that the sin(x) series start with x so again we initialize the sum with x and goes as like the Taylor series.