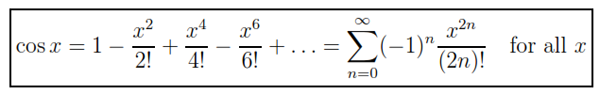Lets try with Taylor and Maclaurin Series. We start by supposing that ƒ is any function that can be represented by a power series:

Let’s try to determine what the coefficients cn must be in terms of ƒ. To begin, notice that if we put x = a in Equation 1, then all terms after the first one are 0 and we get
ƒ(a) = c0
If we differentiate the series in equation 1 term by term...
Here we just convert the degree in radian as we know that
1800 = πc

And the substitution of x = a in equation 2
ƒ'(a) = c1
Now we differentiate both sides of Equation 2 and obtain

Again we put x = a in Equation 3. The result is
ƒ''(a) = 2c2
Let’s apply the procedure one more time. Differentiation of the series in Equation 3 gives

ƒ'''(a) = 2.3c3 = 3!c3
By now you can see the pattern. If we continue to differentiate and substitute x = a, we obtain
Solving this equation for the nth coefficient cn, we get
This formula remains valid even for n = 0 if we adopt the conventions that 0! = 1 and ƒ(0) = ƒ.
Thus we have proved the following theorem.
THEOREM: If ƒ has a power series representation (expansion) at a, that is, if
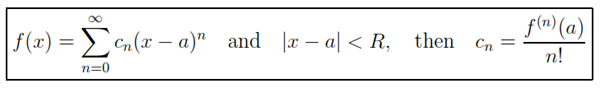
Substituting this formula for cn back into the series, we see that if ƒ has a power series expansion at a, then it must be of the following form.

This equation is called the Taylor series of the function ƒ at a (or about a or centered at a). For the special case a = 0 the Taylor series becomes

This case arises frequently enough that is is given the special name Maclaurin series.
EXAMPLE 1: Find the Maclaurin series for sin x and prove that it represents sin x for all x.
Solution: We arrange our computation in two columns as follows:

Since the derivatives repeat in a cycle of four, we can write the Maclaurin series as follows:

See the C program to find out sin(x)
EXAMPLE 2: Find the Maclaurin series for cosx and prove that it represents cosx for all x.
Solution: We arrange our computation in two columns as follows:

See the C program to find cos(x)
Collected from Calculus Website, by Kiryl Tsishchanka